IntroductionThis measurement and statistical appendix provides a detailed explanation of the measurement and statistical issues involved in the study of dream content. It has a special focus on the Hall and Van de Castle (HVdC) coding system (1966) because of its comprehensiveness and widespread usage by investigators in at least 11 different countries in the first 50 years after it was first introduced. This document gathers together past explanations and analyses that appeared in several different places, and at the same time provides updates and more recent statistical additions, such as discussions of the issues of multiple testing and autocorrelation. It also presents a critique of alternative coding systems and of some of the statistical procedures that are sometimes used in conjunction with content analysis. In making its suggestions and critiques, this appendix makes use of empirical studies to support its points, such as findings on the value of corrections for dream length and on necessary sample sizes. There are two general sections, one on measurement issues, one on statistical issues. The statistical section argues for the most part (but not entirely) that measurement issues dictate the statistics that are used for HVdC codings, and that these statistics are very powerful even while being more intuitive and accessible to those with an everyday understanding of percentages (which are actually better discussed academically as proportions). Measurement IssuesDream reports are a form of text that conveys a narrative. In that general sense, they are similar to a fictional story, a news story in a newspaper, or a person's verbal account of what went on at the county fair on its opening day. In all these ways, dream reports and other texts differ from the information usually collected on most psychological issues — response times in a discrimination task, yes/no answers to a series of questions, expressions of agreement or disagreement on a scale that ranges from 1 to 7. One of the foundational statements of content analysis concluded that its "fundamental objective" is to convert the "symbolic behavior" of people into "scientific data," by which the author meant (1) objectivity and reproducibility, (2) susceptibility to measurement and quantification, (3) significance for either pure or applied theory, and (4) generalizability (D. Cartwright, 1953, p. 466). Thus, the study of dream reports is a form of content analysis. A dream researcher defined content analysis as "the categorization of units of qualitative material in order to obtain frequencies, which can be subjected to statistical operations and tests of significance" (Hall, 1969a, p. 175). It includes four basic steps: (1) creating clearly defined categories that can be understood and applied in a reliable way; (2) tabulating frequencies; (3) using percentages, ratios, or other statistics to transform raw frequencies into meaningful data; and (4) making comparisons with control groups or normative samples. The most crucial issue in content analysis, which shapes most of what follows, is the nature of the categories (scaled or discrete/categorical/nominal) and the preciseness of their definitions. Based on experience, it has been found that it is very difficult, if not impossible, to utilize content categories developed for one kind of text (e.g., literary articles) with another kind (e.g., dream reports) (Hall, 1969a). This hard-won wisdom, based on past failures, has been overlooked by some dream researchers, who still try to adapt content-analysis systems developed for other types of texts, such as psychotherapy transcripts, into ways to study dream content. They thereby ignore the fact that two major compilations of past coding systems are in large part graveyards filled with failed adaptations (Hall & Van de Castle, 1966, Chapter 15; Winget & Kramer, 1979). The first and most frequently used forms of content categories in psychological studies are "scaled" ("hierarchical") categories that are ordered along a continuum, which assumes there are different degrees with a particular dimension. They involve ratings or rankings, including the assignment of "weights," usually in the form of the numbers 1 through 5, or 1 through 7. However, ranking are not meant to imply that the categories along the continuum are equally distant from each other; each stop along the way simply means "more than" or "less than." Such rating systems have proved to be extremely useful in a wide range of waking-life studies, especially concerning attitudes. In some instances they have been equally useful for studying characteristics of dream reports that have parallels with degrees of intensity in waking life, such as the degree of activity or emotional intensity, or for studying dimensions without specific content, such as clarity of visual imagery or vividness (Foulkes, 1982, 1985). Such studies have been especially useful in showing that most dream reports are reasonable simulations of waking life, not a jumble of incoherence, bizarreness, and intense emotionality (e.g., Dorus, Dorus, & Rechtschaffen, 1971; Foulkes, 1985; Foulkes, Sullivan, Kerr, & Brown, 1988; Snyder, 1970; Strauch & Meier, 1996). Rating scales for dream content are constructed with relatively ease, and are not labor intensive to deploy. However, they can be limited in their usefulness for the study of dream content (e.g., settings, characters, social interactions) for a variety of different reasons. They usually do not make a correction for dream length, which often leads to longer reports receiving higher ratings for types of content. In addition, it is often difficult to establish reliability with some scales, which frequently involve subtle judgments about which category along the continuum is the most appropriate, especially when researchers from outside the original investigative team try to use them (Hartmann, Rosen, & Rand, 1998; Winget & Kramer, 1979, p. 179, for examples of difficulties when new raters use the scales). Most importantly, rating scales for social interactions such as hostility/aggression, which assign low numbers to each insult or rejection, and higher numbers to physical attacks, are implicitly assuming, for example, that six or seven insults and angry remarks are the equivalent of one physical attack, which does not make much if any psychological sense (Domhoff, 1996, pp. 30-37; Hall, 1969a, 1969b; Van de Castle, 1969, present critiques of several rating scales for studying dream content). The Measurement Basis for the HVdC Coding SystemTo minimize the problems involved in using rating scales to study dream content, the HVdC system is based on discrete ("nominal") categories, which provide categorical data. They assign no ranks or weights. Instead, they compare various discrete categories as equals and count up the number of tallies for each category to create overall scores. "Indoor" and "outdoor" settings, and "male" and "female" characters, are examples of categories at a nominal level of measurement, with a simple tabulation of frequencies for each category. In addition, no information is lost with nominal categories because numerous categories can be created for different aspects of any complex conceptual category, and then aggregated if need be later in the data analysis. Nor do nominal categories imply the questionable psychological assumptions built into some rating scales. The eight HVdC categories for aggression provide a good example of these two points. Each aggression in a dream report (defined as hostile thoughts toward another character or deliberate, intentional acts by one character to annoy or harm some other character) is tabulated into categories ranging from (1) covert feelings of hostility to (2) verbal criticism to (3) rejection or coercion to (4) verbal threat of harm to (5) theft or destruction of a person's possessions to (6) chasing, capturing, or confining to (7) attempts to do physical harm to (8) murder. The frequencies for each category can be compared with normative findings with large samples. Categories one through four, the nonphysical types of aggression, can be summed, as can categories five through eight, the physical aggressions. Finally, all categories of aggressions can be totaled for an overall aggression score. There is no information lost in this system, and there are no assumptions about how much "stronger" or "heavier" or "weightier" one aggression is compared to another Discrete categories also make it possible to use specific elements within the dream reports as the unit of analysis in statistical analyses. This leads to a series of "content indicators," based on proportions and ratios. For example, to draw an example from the aggression categories, a content indicator called the Physical Aggression Percent can be created by dividing the total number of physical aggressions in a given sample of dream reports by the total number of aggressions (nonphysical aggressions + physical aggressions). This indicator reveals that the Physical Aggression Percent is higher for men than for women in most nation-states and smaller pre-industrial societies (Domhoff, 1996, Chapter 6 for details). Similarly, the percentage created by dividing the total number of male characters by the total number of male and female characters leads to the "Male/Female Percent" (M/F%), which is usually about 67/33 for men and 48/52 for women in most societies across the world, with the difference appearing as young as ages 5-6 in one laboratory study (Domhoff, 1996, Chapters 5 and 6; Hall, 1984). These and many more content indicators are listed in Table 1, along with the simple formulas for calculating them. It is important to note that some of these indicators have proved to be more useful than others, but that some of those that are less frequently used have proven to be valuable in specific studies. Thus, investigators have to determine for themselves which of the indicators are best suited to answer their questions. It also needs to be said that the frequencies for some indicators are very small, such as for the Unusual Character Percent (the sum of dead characters, imaginary characters, fictional characters, creatures, and characters that morph into another character, divided by all the characters found in the sample). At the same time, the Unusual Characters Percent has been useful in detecting an interest in TV characters or fictional book characters (e.g., the Harry Potter series) in a few individual case studies. Then, too, some of the past indicators, which were based on compilations of many categories ("meta-indicators," so to speak), sometimes obscured more than they revealed, so they are no longer included on the list. Finally, some of the indicators on the list never have been used, such as the Distorted Setting Percent and the Confusion Percent.
Table 1. The formulas for calculating the Hall/Van de Castle content indicators
Adapted from Domhoff (2003).
It is also sometimes possible to encompass or call into question other coding systems by combining two or more HVdC categories into new scales. This point has been demonstrated by a comparison with findings from a mislabeled and unvalidated "masochism" scale, which is one of the few content scales other than the HVdC system that has been used by researchers not involved in its creation (Beck & Hurvich, 1959). The scale consists of a wide range of negative experiences ranging from physical discomfort to rejection to being punished, lost, or victimized. Using this scale, one investigator came to the conclusion that divorced women who are not depressed are more masochistic than divorced men who are depressed (R. Cartwright, 1992). This is a surprising result that seems to raise more questions than it answers. However, in a very useful study, Clark, Trinder, Kramer, Roth, and Day (1972) already had shown that the items on the purported "masochism" scale are encompassed by three categories in the HVdC system: failures, misfortunes, and victim status in aggressive interactions. They then demonstrated this point by coding two different samples with both the "masochism" scale and the three HVdC categories. They found that the masochism findings are encompassed by the Hall/Van de Castle categories, which also picks up several elements missed by the "masochism" scale. Since women are slightly more likely to fail when they strive in dreams, and to be victims in aggressive interactions, the greater "masochism" that Cartwright (1992) reports in her women participants is really a combination of failures and victimizations, which are not obvious manifestations of clinical masochism. Moreover, the HVdC misfortune categories, which might plausibly be related to masochism because they involve negative things that happen to people out of the blue, show only small gender differences, appearing in 36 percent of men'sdreams and 33 percent of women's dreams. Over and beyond the breadth of dream elements that are covered by the HVdC content indicators, and the possibility of combining them in new ways, content indicators are also important because they help achieve the greater quantitative precision and sample comparability that are necessary for two basic reasons. First, and most crucially, there are wide individual differences in report length, and women's dreams are often found to be longer than those of men (Bursik, 1998; Hall & Van de Castle, 1966; Winegar & Levin, 1997). Varying lengths are a problem because longer reports are likely to have more of most things in them, although one study reported that the relationship is not monotonic for all categories in the HVdC system (Trinder, Kramer, Riechers, Fishbein, & Roth, 1970). There is a further problem beyond the length of dream reports in making sample comparisons more precise: dream reports can vary from group to group or individual to individual in the frequency with which certain elements appear, even when report length is held constant. This difference in "density" seems to be especially the case for the frequency of characters, which means that there is more likelihood of social interactions in some dream reports than others. Once again, there is a gender difference. There are usually more characters in women's reports, an interesting finding in and of itself, but one that has be taken into account in analyzing social interactions (Hall, 1969a, 1969b). The difference in the density of characters can be controlled by the use of the three social-interaction ratios listed in Table 1, which involve dividing the total number of aggressive, friendly, or sexual interactions by the total number of human characters, to create an aggressions/character ratio (the A/C Index), a friendliness/character ratio (the F/C Index), and the sexual interactions/character ratio (the S/C Index). A control for character density also is provided by one of the percentage indicators, the "Aggressions/Friendliness percent" (A/F%), which is tabulated by dividing all the aggressions in a sample by all the aggressions plus all the friendly interactions. The social-interaction ratios and the A/F% also can be determined for types of characters, such as men, women, teenagers, or children, as well as for specific characters, such as the dreamer's mother or father. The alternative strategies utilized in other coding systems for correcting for differing report lengths and character densities are sometimes cumbersome or of questionable utility, and often opaque to behavioral and brain scientists outside the field of dream research, and to general readers as well. For example, using the mean number of words or lines per dream report as the unit of analysis does not deal with the differing "wordiness" of participants, and leads to unwieldy findings such as "there were 2.3 human characters per every ten lines (or 100 words) in the dream narratives." Nor does this approach take into account that more complicated or unusual elements might take more words to describe, which means that dividing by the number of words could wash out real and important differences, especially in studies concerned with creativity or unusual features in dreams (Hunt, Ruzycki-Hunt, Pariak, & Belicki, 1993). A Successful Correction for Dream LengthNormative studies of large samples of dream reports from college men and women, which were coded for most of the HVdC categories, make it feasible to conduct methodological studies that demonstrate the usefulness of percentages and ratios in correcting for differences in report length and character density. Such corrections for report length are necessary because there are correlations between the number of words in dream reports and the frequency of some elements. This is especially the case for elements that are seldom analyzed in detailed, such as the number of activities and objects in dreams, but it is also a serious issue with the number of characters, emotions, aggressive interactions, and friendly interactions in both the male and female normative samples (Domhoff, 2003, p. 81, Table 3). In the HVdC normative dream sample for women, for example, the number of words and the number of characters correlate .45, words and emotions correlate .27, and words and aggressions correlate .20. Three different studies — one using the HVdC male norms, another the HVdC female norms, and a final one using dream reports on DreamBank.net from a woman code-named "Barb Sanders" — confirm that the content indicators are successful in eliminating any biases created by report lengths that vary from 50 to 500 words. First, a comparison of dream reports with 50 to 175 words with reports with 176 to 300 words in the three sets of dream reports found that there are no systematic differences between shorter and longer dreams on any of the percentages and ratios when the samples are compared. The Physical Aggression Percent for women was unexpectedly lower in the longer dreams, and the Familiar Settings Percent (familiar settings divided by all settings) was lower in the men's dreams, but the same differences were not found in the other two samples. Similarly, the Bodily Misfortunes Percent (all misfortunes that happen to the dreamer's body divided by all misfortunes that happen to the dreamer) was lower for Barb Sanders in the longer dreams, but the same difference did not show up with the other two samples. On the other hand, and as expected, the longer dreams are usually higher on the seven "At-Least-One" indicators presented in Table 1 (which include aggression, friendliness, sexuality, misfortune, good fortune, success and failure). Since these indicators simply provide the percentage of dream reports that have at least one instance of any of these seven categories, they do not control for length. The largest study of the issue of dream length is based on 3,115 dream reports in the Barb Sanders series (Domhoff, 2003, Chapters 3 and 5; 2010). The starting point for the study of dream length was a random sample of 250 dream reports from that series, which ranged in length from 50 to 300 words. These reports were coded for characters, social interactions, misfortune and good fortune, and emotions. Then random samples of 200 shorter and 200 longer dream reports were added to the original sample of 250. These samples of shorter and longer dream reports were only coded for social interactions, which are the most important and sensitive coding categories. As might be expected based on earlier comments, the At-Least-One indicators rise consistently as word length increases, but there was an unexpected plateau at 400 words. Still, this finding shows that longer reports have more social interactions as they rise from 50 to at least 400 words, as most researchers might expect. It is also very likely that most other coding categories would show the same sensitivity to report length. On the other hand, none of the percentage or ratio indicators is affected by dream length once a minimum of 50 words is reached, which means that the indicators do an excellent job of controlling for dream length up to at least 500 words, a length that is rarely exceeded in dream reports (Domhoff, 2003, Figure 3.2). But the results also make clear that the content indicators do not do a good job of correcting for the distortions that appear in dream reports of 25 to 49 words. The findings for dream reports from adults that are under 25 words in length are even more distorted. This reinforces the earlier decision by Hall and Van de Castle (1966) to exclude dream reports shorter than 50 words in studies of teenagers and adults. Thus, these indicators have to be used selectively and with care with young children, starting with pre-schoolers around the age of 4 or 5, because their dream reports are usually well less than 50 words. Later studies suggest that report length can reach standards acceptable for HVdC codings by the fifth or six grade (Domhoff, 2018, Chapter 4). The study of young children's dreams is an important instance in which simple frequency counts, rating scales, and At-Least-One indicators, may be more useful than detailed quantitative studies of dream content, as longitudinal and cross-sectional laboratory studies of children ages 3-9 have shown (Foulkes, 1982; Foulkes, Hollifield, Sullivan, Bradley, & Terry, 1990). The Issue of ReliabilityGiven the seeming complexity of the HVdC coding system, which is more apparent at first glance than real, the question arises as to whether two coders make the same decisions in coding a set of dream reports, or if the same coder makes similar decisions during a second coding three months or more after the original one. This is the measurement issue of reliability, which can be defined as consistency between coders, or the consistency of the same coder at two distant time periods. Many studies show that the HVdC system has very high reliability using the percentage-of-agreement method as the reliability indicator. This reliability indicator is calculated by dividing the total number of codings for a specific category or subcategory (e.g., aggressions, types of nonphysical aggressions, or types of physical aggressions) on which two coders agreed, by the total number of coding agreements plus the total number of disagreements between them. For example, if coder A made 47 codings for murder (A8) and coder B made 48 codings for the same category, and they agreed 45 times, then the percentage of agreement would be 45 divided by 50 (i.e., 45 + 2+3 )= .90. The percentage of agreement is a standard reliability measure for all types of content-analysis studies in the social sciences (e.g., Smith, 2000). It is also the one that makes the most empirical sense with the HVdC system based on a comparison with the results provided by several different methods of determining reliability for the same set of codings (Hall & Van de Castle, 1966, Chapter 13). Using other methods to assess reliability with the same codings, the reliability coefficient could vary from very low to 100 percent (Hall & Van de Castle, 1966, pp. 147-148). In particular, Hall and Van de Castle's comparisons show the dangers of using a correlation coefficient with the HVdC coding system because it does not answer the question of how often the two judges agreed exactly on their codings; they then demonstrate the superiority of the percentage-of-agreement method by making direct comparisons with the results using correlation coefficients (Hall & Van de Castle, 1966, pp. 148-151, 154-155). In general, correlation coefficients inflate reliability, conveying a false sense of precision. The high level of reliability using the percentage-of-agreement method, with its focus on specific coding categories and subcategories, and with an explicit assessment of disagreements, is due for the most part to the clarity of the rules for classifying elements. However, in recent years reliability has been improved for new users of the system by the addition of two online sets of coded dream reports to dreamresearch.net for training purposes. One sample was coded in the early 1960s by both Hall and Van de Castle for their methodological book (1966, Appendix B), the other sample in the late 1990s by two coders as part of a study of dream reports from boys and girls ages 12-13 (Avila-White, Schneider, & Domhoff, 1999).They can be found on dreamresearch.net: http://dreamresearch.net/Examples/ Although the percentage-of-agreement method contains the least assumptions and has been shown to work well with the HVdC system, some investigators use a slightly different reliability measure, kappa. This measure was created in an attempt to correct for chance agreement by two raters who are guessing at least some percentage of the time in making clinical diagnoses, which usually involve "yes" or "no" type of judgments of protocols or x-rays (Cohen, 1960). It is a relatively simple measure and is available in software packages. However, there are strong criticisms of it as a general index of reliability. It is not really chance-corrected due to the fact that such a correction implies a model of how raters are making their decisions. If its assumptions are violated, major distortions can result. Further, as a general (omnibus) measure, it does not pinpoint the sources of disagreement, and it can vary depending on whether few or many codings are made (Uebersax, 1987; 2014b, for a summary and a full bibliography). Nor are HVdC coders guessing; they are making informed choices that may be off by only one subcategory in some cases, such as whether an aggression is an A2 or an A3, so using a chance correction based on the number of coders' disagreements makes no conceptual sense given the nature of the explicit rules for HVdC codings. Using kappa violates the rule of "Keep it simple," concludes one statistician who has studied the issue with care. "All other things being equal," he continues, "a simpler statistical method is preferable to a more complicated one. Very basic methods can reveal far more about agreement data than is commonly realized" (Uebersax, 2014a). Although the percentage of agreement method does not take into account the probability that two coders will agree by chance, this formal statistical issue does not seem to be an important one when coders are not forced to choose an option. That is, each coder first has to decide that there is, for example, an aggression or a friendliness, and then decide on the appropriate category. When the intricacies of the HVdC coding system are taken into account, along with the several hours of training and practice that it requires, it is unlikely that even a complex reliability measure can correct for any unknown probabilistic contingencies. Thus, just as with the use of proportions with HVdC data, the use of the percentage-of-agreement method makes the most intuitive sense and has the further advantage that it is understandable to everyone (Hayes & Hatch, 1999). The perils of kappa and the advantages of using the percentage-of-agreement method aside, the coders carrying out HVdC codings should discuss any differences and resolve them after they are finished so there is one set of codings to be used in the statistical analysis. This process also improves the quality of the codings if the coding rules and examples are consulted for each case. When possible, it also makes sense to have a more experienced coder resolve the disagreements by reading through and recoding the dream reports on which there were disagreements. Serious coding takes time, which people are often wont to invest when so much can be done by software, but most HVdC coding categories are too complicated to be coded with word strings or other computerized methods, and usually provide better and more useful results. Emotions are one important exception to that generalization, although there are a few other exceptions for frequent elements such as activities, objects, natural elements, and other HVdC categories seldom coded due to time constraints (Bulkeley, 2014; Domhoff & Schneider, 2008b). The Statistical Rationale for Analyzing HVdC DataThe percentage and ratio indicators used in the HVdC system to control for report length and character density are best analyzed with the test for the significance of the difference between two independent proportions. This deceptively simple statistic is in fact a type of mean for which all the values in the distribution are either zero or one. For example, if four out of 10 dream reports contained an instance of apprehension, which is a proportion of 4/10= .40, the same result could be reached if reports with apprehension were coded as "1" and reports without any apprehension were coded "0." The mean of these 10 scores of 0 or 1 would be (0 + 0 + 1 + 0 + 1 + 1+ 0 + 0 + 0 + 1)/10 = .40. Basically, a proportion only seems simpler than a mean because it is familiar to everyone from an early age in the form of a "percentage," which is simply a proportion multiplied by 100. In any case, the important point is that "the same kind of inferential issues" are involved with proportions as with means in general, as stressed by one of the most prominent contributors to psychological statistics in the second half of the twentieth century: A proportion is a special case of an arithmetic mean, one in which the measurement scale has only two possible scores, zero for the absence of a characteristic and one for its presence. Thus, one can describe a population as having a proportion of males of .62, or, with equal validity (if not equal stylistic grace), as having a mean "maleness" of .62, the same value necessarily coming about when one scores each male 1, each non-male 0, and finds the mean. (Cohen, 1977, p. 179; see Ferguson, 1981, p. 185, for agreement) Given the fact that the same logic underlies both mean-difference and proportional-difference testing, nothing would be gained by determining the mean number of characters or emotions or aggressions per dream, even if the calculation of means did not have the aforementioned problems of cumbersomeness and opacity due to the differing lengths of dream reports from sample to sample. It is also the case that another frequently used statistic, chi-squared, provides the same results as the proportions test for the 2×2 categorical tables that are most frequently used with the HVdC system. Chi-squared is a very versatile and useful statistic because it can be used to analyze tables with many than two rows and columns, but it yields the same results with a 2×2 table as the test for the significance of differences between proportions. That is, the "z" score derived from a proportions test is equal to the square root of chi-squared (Ferguson, 1981, pp. 211-213). Moreover, the proportional difference between two samples is exactly equal to the Pearson r between the two samples (Rosenthal & Rubin, 1982). For example, a difference of .13 between two samples can be understood as an r of .13 between two dichotomous variables. Thus, there is nothing to be gained by working with chi-squared or correlational statistics instead of proportions with the data provided by HVdC content indicators. Based on the admonition that "simpler is better" even when complex designs are possible (Cohen, 1990, 1994), most studies of dream content using HVdC codings have relied on the comparison of two groups. This approach maximizes the size of the samples in each cell, avoids confounds, and minimizes reliance on complex statistical analyses, which usually are based on several assumptions that may or may not hold for any given sample, and therefore have potential weaknesses. However, in the case of studies that analyze three or more variables, it is possible to use other basic statistical test that are often deployed with categorical data, such as chi-squared, the Wilcoxon signed-rank test, Krusak-Wallis one-way analysis of variance, and Friedman two-way analysis of variance. For example, Hall (1966) used the Wilcoxon signed-rank test to compare HVdC codings for dream reports from several different REM periods, which led to the conclusion that there were no differences in dream content from REM period to REM period, and Strauch (2005; 1999) used non-parametric analysis of variance tests in her longitudinal study of the dream content of youngsters ages 9-15. Determining the Magnitude of Effect SizesThe use of the statistic for the significance of the difference between two proportions leads seamlessly to the use of an effect-size measure called h, which is similar in its general logic to the better-known d statistic for determining effect sizes based on means; both of these statistics were created by the same statistical psychologist (Cohen, 1988). In principle, the difference between the two proportions is the "effect size." However, due to the fact that the population parameters are unknown with proportions, it is not possible to compute standard deviations, so the size of the differences at the extremes of the sampling distribution is not actually the same as it is in the middle of the distribution. This statistical point, which is not easily translated into words, essentially means that the actual size of the difference between, say, .02 and .08 (.06) is not the same as the difference between .44 and .50 (.06), which are in the middle of the range (Cohen, 1977, p. 180, for the statistical explanation). Look-up tables provide the needed corrections for each sample and make it possible to subtract one correction from the other to derive h (Cohen, 1977; Domhoff, 1996, p. 315). Even better, the h statistic itself is calculated by the DreamSAT spreadsheet that is available on dreamresearch.net for doing all the statistical calculations for a full HVdC analysis once the codings are entered into it. ("SAT" stands for "statistical analysis tool.) Thus, using DreamSAT makes the use of the tables unnecessary. Generally speaking, h is a little more than twice as large as the percentage difference between two samples when the proportions for the two samples are between .15 and .85. It is only at the extremes that h becomes increasingly larger than about twice the difference between the two proportions. The h statistic has the added value that it provides an effect size that is equal to phi and lambda, the two statistics used to determine effect sizes with chi-squared (Ferguson, 1981; Reynolds, 1984). Then too, the magnitude of the difference between two proportions is equal to the Pearson r for dichotomous variables, so nothing is gained by using a correlational approach instead of percentages (Rosenthal & Rubin, 1982). Thus, r=phi=lambda=h in terms of effect sizes with 2×2 tables. The determination of what is a "small," "medium," or "large" effect size varies from research area to research area and is in good part a judgment based on experience. Cohen (1977, p. 184) suggests that a good starting point is to consider h=.20 a small effect size, h=.40 a medium effect size, and h=.80 a large effect size, but he also urges researchers to "avoid the use of these conventions" if they can substitute "exact values provided by theory or experience" in the specific area in which they work. Despite Cohen's explicit call for the use of experience in each research area as the best guide to using terms such as "small," "medium," and "large," his suggested starting point has tended to become an accepted standard even though studies show that the general range of effect sizes varies greatly from subject matter to subject matter. However, based on experience with past HVdC findings, effects sizes up to .20 should be considered small, effect sizes from .21 to .40 are best thought of as medium, and effect sizes above .40 are large. Effect sizes of .50 or above have been extremely rare in studies of dream content except in a few individual case studies (Domhoff, 1996, Chapter 8; 2003, Chapter 5). To provide some perspective on the relative magnitude of these effect sizes, Table 2 presents the mean effect sizes that Rosnow and Rosenthal (1997) calculated for several areas of psychological research, along with the equivalent h values I calculated for comparisons with findings from dream research. This table shows that effect sizes vary considerably from research area to research area, which makes the case that each research area should determine what is a small, medium, or large effect size. The table also shows that the effect sizes in HVdC studies are in the middle of the range.
Table 2. Effect sizes in selected areas of psychological research
From Domhoff (2003).
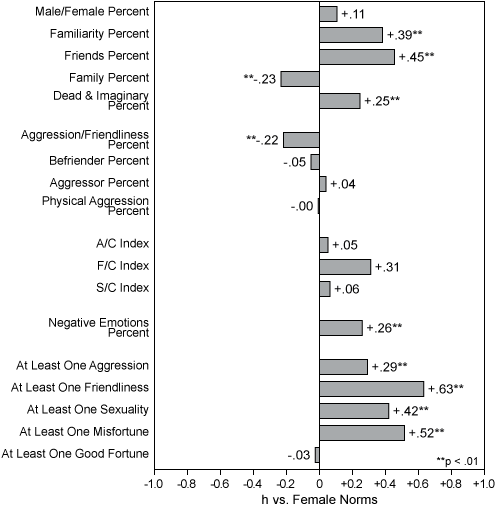
There is good reason to believe that h works just as well with the "repeated measures" of a long dream series from one person as it does with independent samples. This claim derives from a simulation study using 10,000 resamples (each time a pair of scores are drawn from the larger pool based on two samples, and then they are return to the pool, making it possible that they will be used additional times in the simulation). The simulation shows that Cohen's formula for determining the effect size between two independent means, d, produced almost exactly the same results with correlated measures as did a more complex formula that takes into account the size of any correlation between two samples. Since proportions are a special case of the mean, this result holds for h as well. Although the authors conclude that the more complex equation also used in their simulation study is "consistently slightly more accurate," they also note that "the differences are quite small and are trivial for the sample size of 50" (Dunlap, Cortina, Vaslow, & Burke, 1996, p. 172). Since the differences derived from the two equations are small, and sample sizes are almost always over 50 in Hall/Van de Castle studies, it is feasible to use h for both independent and repeated-measures studies of dream content. This is an important conclusion that further strengthens the case for the increased use of individual's dream series in future research studies. The h statistic also makes it possible to present results in a clear graphic representation as well as in standard tables, because the effect sizes for all or any subset of the HVdC indicators can be placed on a bar graph that resembles an MMPI profile. This "h-profile" immediately reveals through visual inspection the comparative size of the h differences between any two samples on the content indicators that are being used. When new samples are regularly compared with normative samples, it is possible for those researchers familiar with past results to determine very quickly if there are any consistent patterns for particular types of individuals or groups. For example, the h-profile in Figure 1 shows the dream reports of one 15-year-old girl, which differs from the HVdC women's norms on several indicators having to do with characters and social interactions.
Figure 1. Bea at Ages 14-15, compared to the Female Norms
Confidence intervals are used to estimate the range of values within which findings from additional samples would fall with a certain degree of probability. They are strongly advocated by psychological statisticians as a better way to present statistical findings, and indeed, as a substitute for significance testing (Cumming, 2012, 2014a; 2014b, p. 21). This emphasis can be easily incorporated into research on dream content by using the h statistic as a starting point. In effect, confidence intervals are the inverse of p values (levels of significance), which state the probability that new samples will fall outside the confidence interval. A 95% confidence interval is the complement of a p value of .05, and a 99% confidence interval is the complement of a p value of .01. The advantage of confidence intervals is that their width makes clear just how much variability there is likely to be in h from sample to sample. The narrower the CI, the more impressive the finding. Approximate Randomization Cross-Validates the Use of ProportionsThe accuracy of proportions in determining p values has been demonstrated by comparing their estimates to those based on the computationally intensive randomization strategy called approximate randomization. Like the nonparametric statistics to which they are closely related, randomization strategies bypass most of the assumptions that are in theory necessary for the use of parametric statistics (e.g., Franklin, Allison, & Gorman, 1997; Hager, 2013; Noreen, 1989; Sherman & Funder, 2009). Specifically, there is no need for random samples, similar sample sizes, or a normal distribution of scores. Through the use of random resampling (carried out by randomly drawing thousands of pairs of samples from a common pool made up of values from both samples), randomization provides exact p values, not approximations. Randomization strategies do assume that the samples being compared have similar shapes and variances, but that is true for parametric statistics as well (Franklin, et al., 1997). Many parametric statistics are very robust in the face of one or more deviations from their underlying assumptions (e.g., Gaito, 1980; Gleason, 2013; Norman, 2010), which is contrary to my unfortunate partial conflation of measurement theory and statistical theory in two earlier overviews of the statistics used with the HVdC coding system (Domhoff, 2003, pp. 63-64; Domhoff & Schneider, 2008a, pp. 1258-1259). However, large sample sizes can make nonparametric and randomization strategies just as powerful, in the sense of accurately detecting a real difference when there is one. In fact, nonparametric tests can be even more powerful than parametric tests with highly non-normal data. And in one simulation study, randomization statistics were more powerful than both the nonparametric Wilcoxon signed-rank test and the parametric t test when distributions were skewed (Keller, 2012). This point is critical for dream research because very few of the elements in dream reports are normally distributed. Instead, there is often a highly negative skew to distributions. It is also important to emphasize that randomization techniques work equally well with longitudinal studies of individual dream series because there is no assumption of independence (Franklin, et al., 1997). This conclusion once again strengthens the case for the use of the lengthy individual dream series that have proven very valuable in dream research, revealing the consistency of dream content over time and the continuity of dream content with waking personal concerns about important people and interests in the dreamers' lives (e.g., Bulkeley, 2012; Domhoff, 1996, Chapter 8; 2015). The program for approximate randomization, available on request through dreamresearch.net, determines exact p values by — to repeat for clarity's sake what was said earlier in different terms — pooling (i.e., merging) the data from both of the samples and then creating 5000, 10,000 or even more new pairs of random subsamples. The p value is the percentage of times that the difference between a pair of randomly drawn subsamples is equal to or greater than the difference between the two original samples. For all but the few HVdC content indicators for elements that appear very infrequently, approximate randomization returns about the same p values as the proportions test, thereby demonstrating that the proportions test is providing accurate p values in almost all instances (Domhoff, 2003, pp. 85-87; Domhoff & Schneider, 2008a). For example, a comparison of the M/F% for men (67/33) and women (48/52) found there were only 6 instances in 5000 trials in which the difference between the randomly drawn pairs of samples was equal to or larger than the difference between the two original samples, so the p value is .0012 (6 ÷ 5000 = .0012). However, when the same comparison is made using content indicators with small differences between two very small percentages (less than 10 percent), discrepancies between the two methods for determining p values are revealed. The standard formula sometimes indicates that the results are significant at the .05 or .01 level of confidence, but approximate randomization shows that the results are not significant at either of those levels. In such cases, the formula is wrong because the dream elements being studied only appear a small number of times, which creates distortions with distributions that are expressed in proportions. Precise confidence intervals can be determined by means of a randomization strategy called "bootstrapping," which makes it possible to determine confidence intervals with great precision. As with other randomization statistics, the basic idea is to draw 1,000 or more resamples and examine the distribution of outcomes, this time using "resampling with replacement." (Resampling with replacement simply means that each value that is drawn randomly from the pool of values is returned to the pool, which makes it possible a value might be used several times in the course of drawing the sample.) The basic assumption is that these resamples "are analogous to a series of independent random samples" (Mooney & Duval, 1993, p. 11). Simulation studies using samples with known parameters support this assumption. They also show that bootstrapping provides more accurate confidence intervals than do standard formulas that assume normal distributions based on randomly drawn samples. Bootstrapping also allows confidence intervals to be asymmetrical when a distribution is skewed, something that is not possible with the standard formula. The approach to calculating bootstrapped confidence intervals most frequently used by applied statisticians, the percentile method, is ideal for use with the HVdC content indicators because it is consistent with the use of proportions for determining p values and effect sizes. In addition, the other methods either revert to parametric assumptions or require hundreds of thousands of resamples with replacement for very little gain (Mooney & Duval, 1993). Although the percentile method is of limited usefulness with samples of less than 30, and requires 1,000 or more resamples, these potential problems are not relevant for HVdC analyses. This is because studies of dream content require large sample sizes for reasons demonstrated in more detail in the next section. It is also the case that the resampling utility on dreamresearch.net (which is available to anyone on request) can analyze 10,000 or more resamples in a matter of seconds. To set the 95% confidence interval, the bootstrapping program first generates a value for each of the 10,000 resamples of the indicator being studied. Next it counts down from the largest value in the distribution to the 125th largest value, and then up from the smallest value to the 125th smallest value. The 125th largest value and the 125th smallest value are the 95% confidence interval with 10,000 resamples. (In other words, 5% of 5,000 equals 250, with half of the 250 at one end of the distribution, the other half at the other end.) The Issue of AutocorrelationAutocorrelation in time series data (i.e., the lack of independence among a series of responses from a single individual) is an issue in several different areas of psychology because most statistical tests are based on the assumption that each response is an independent data point. In psychological studies, autocorrelation is thought to be increasingly likely as the time between responses decreases because it becomes more plausible that the prior responses — and/or some underlying factor(s) — are influencing subsequent responses. This possibility is most apparent in dream research in the use of dream series, which have provided several important findings and may be of even greater value in the future (Domhoff & Schneider, 2015a, for a full discussion). Wald and Wolfowitz's (1940) runs test, a statistical technique designed to test for randomness in categorical time-series data, can detect the presence of any form of dependency within a dataset, including monthly or seasonal cyclical patterns. It is the best-suited test for categorical data because the frequently used Durbin-Watson test assumes at least an interval level of measurement. The Wald-Wolfowitz test determines whether or not there is any pattern in the runs that appear (with a run defined as one or more similar observations followed by one or more dissimilar observations). The runs test's ability to detect nonrandomness is greater with longer datasets. In addition, the p-value for the runs test can be supplemented with a one-period lagged phi coefficient (a measure of correlation between two categorical variables) to provide a descriptive measure of the strength of the first-order autocorrelation. The one-period lagged phi coefficient is computed from a 2×2 contingency table with the binary responses for period t as rows and the binary responses for period t+1 as columns. The lower the first-order autocorrelation, the more likely it is that the Wald-Wolfowitz results are solid ones. The application of the runs test begins by counting the observed number of runs and comparing them with the expected number of runs — the latter via a formula that takes into account the number of runs and the overall frequency of occurrence for each type of observation. Using a formula based on the difference between observed and expected proportions, a Z score and p value are calculated. A utility for the runs tests is available to other dream researchers upon request via dreamresearch.net. It takes plain text as input, with observations represented by single characters and separated by white space or commas. The output includes the observed and expected number of runs, a Z score, and a p value. In a study of five different dream series, 125 runs tests were carried out on dream reports coded for various HVdC categories. This analysis resulted in six statistically significant results, five at the .05 level and one at the .01 level. The percentages of statistically significant differences that were found — 4.8 percent at the .05 level and 0.8 percent at the .01 level — are close to what would be expected by chance. However, because the failure to reject the null hypothesis of randomness can be due to either the brevity of a time series or very weak autocorrelation, the one-period lagged phi coefficient was also computed for each dream series. These first-order phi coefficients were extremely small, which suggests that the results of the Wald-Walkowitz test are accurate. Nor is it likely that the many nonsignificant results are due to a lack of statistical power. This is because the power of the runs test depends on the length of the time series, all of which were long in this study as compared to most time series that are analyzed, ranging from 86 to 171 dream reports. The overall nonsignificant results are therefore most likely due to extremely weak autocorrelations within each dream series. The overall results for the Wald-Walkowitz tests and the phi coefficients are presented in Table 3.
Table 3. Wald-Wolfowitz runs tests (p values & phi coefficients) for various Hall/Van de Castle content elements in ten long dream sets from four different dream series
From Domhoff & Schneider (2015a). p-values are in regular type; first-order (AR(1)) phi coefficients are in italics. The number of sets, number of dreams per set, number of categories analyzed, and number of tests carried out are below the names of each dreamer.
*p < .05 **p < .01
Based on these results, it is very unlikely that autocorrelation will be found in future dream series that have been carefully checked for their authenticity to avoid hoaxers. However, if there are any doubts about any given series dream series, it can be checked for autocorrelation with the utility available through contacting dreamresearch.net. On the rare chance that autocorrelations are ever found, it would be necessary to used mixed-effects methods, which are designed to analyze repeated measures that are correlated (Klingenberg, 2008). When the results on the absence of autocorrelation are added to the evidence presented earlier in this article that there are no statistical problems in studying dream series with the HVdC categories, the path is clear for greater use of this invaluable source of nonreactive, unobtrusive archival data, which already has led to many findings about dream content that might not have been possible otherwise. Ratios, Proportions, and the HVdC Ratio IndexesThe fact that randomization statistics replicate results with the proportions test, along with the fact that the runs test demonstrates dream content is independent from dream report to dream report, provides the basis for discussing another important statistical issue. What is the best way to analyze findings from the three HVdC social-interaction ratios (the A/C, F/C, and S/C indexes)? The combination of results from the randomization and autocorrelation studies show that statistical comparisons of results with these three indicators can be carried out with the formula for the significance of the difference between two independent proportions. However, this conclusion has to be supplemented with a more theoretical discussion of the issue to avoid misunderstandings. This is because the relationship between a ratio and a proportion is not always clearly articulated, which can lead to concerns that the proportions test should not be used with ratios. That is, proportions are sometimes thought to be different because they are parts of a whole, such as the proportion of the apple crop that is lost to disease, which can only range from from zero (0%) to one (100%). Ratios, on the other hand, can compare any two quantities — such as the number of trees to the number of benches in a park, which might yield a ratio of 10:1. But as stressed by statisticians, ratios are the more general category because ratios are defined as a comparison of any one quantity to any other quantity, and they can vary between zero and infinity. Thus, a proportion is simply one kind of ratio, but it is a ratio that only can vary between zero and one. It is therefore possible to use the proportions test with a ratio as long as (1) it varies between zero and one, as the HVdC social-interaction indicators always do for any sample with more than a handful of dream reports, and (2) each observation has been shown to be independent of the others, which is demonstrated in the case of the HVdC coding system by the results with the runs test that were presented in the previous section and in Domhoff and Schneider (2015a). The Issue of Multiple TestingMultiple tests of the same pair of samples can greatly increase the probability of finding at least one statistically significant difference by chance. For example, if ten comparisons are made, there is a 40 percent probability of at least one statistically significant difference (i.e., where p < .05) occurring just by chance. This result also can be described as a 40 percent probability of a false positive, which is generally called a Type I error in statistics. With 20 tests, which is a realistic number when using the HVdC system, the probability of at least one false positive at the .05 level rises to 64 percent. However, as far as the HVdC normative findings on differences between men and women on several content indicators, they are first and foremost validated by replications of them with dream samples from the University of Richmond in 1980, the University of California, Berkeley in the mid-1980s, and Salem College in Winston-Salem in the late 1980s (Dudley & Fungaroli, 1987; Dudley & Swank, 1990; Hall, Domhoff, Blick, & Weesner, 1982; Tonay, 1990/1991). But it is also the case that they are preserved after a correction for multiple testing is applied, as discussed later in this section and as demonstrated in detail elsewhere (Domhoff & Schneider, 2015b) To correct for multiple testing with the HVdC system, the Benjamini-Hochberg correction (1995), is used because it controls for false positives by focusing on the comparisons that yielded statistically significant differences. It does not suffer nearly as much from the large loss of statistical power that is experienced when the entire list of p values is used in making the correction whether they are significant or not, as in the case of the earlier Holm-Bonferroni correction (Holm, 1979). Due to its statistical shortcomings, the Holm-Bonferroni method has been widely criticized by statisticians and by practitioners in epidemiology, ecology, and medicine on the grounds that it stifles the further exploration of unexpected findings (e.g, Ellis, 2010; Moran, 2003; Perneger, 1998). This is particularly the case in fields that are primarily at a descriptive stage in the theory-building process (Rothman, 1990). The Benjamini-Hochberg correction is also more useful because it works equally well even when some of the tests are correlated — especially when they are positively correlated (Benjamini & Yekutieli, 2001; Genovese, 2002). It is the method of choice for many researchers in fields such as astronomy, ecology, and molecular biology, which sometimes make hundreds or thousands of statistical comparisons in a single study (Garcia, 2004). It also makes intuitive and statistical sense for dream research because the field is still primarily in an exploratory and descriptive stage (Domhoff & Schneider, 2015b, for a detailed comparison of the two alternative methods that is discussed based on the statistical terminology that is used in discussions of this issue in the statistics literature). The Benjamini-Hochberg correction can be carried out using a program for it that is attached to DreamSAT on dreamresearch.net. Along with information on whether or not an initially significant difference is preserved for each indicator, the results include an adjusted p value for each indicator as well. Although statisticians do not consider the determination of each adjusted p value to be necessary, the inclusion of "before-and-after" p values in a table makes it possible for those who doubt the usefulness of any correction formula to decide for themselves whether or not they want to take the multiple-test adjustment into account. The tables also include p values for content indicators that were not significant before the adjustment was made. These values are useful because researchers who are familiar with the HVdC norms can see if the patterns of significance and non-significance found in future studies are familiar to those found in the past. The impact of the multiple-comparison correction on dream content studies using a large number of HVdC indicators was first examined by means of a reanalysis of the normative findings for men and women, using p and h values calculated using DreamSAT. Although DreamSAT includes 28 Hall/Van de Castle content indicators, six were omitted from this analysis for the following reasons: the spreadsheet does not calculate p and h values for the A/C, F/C, and S/C indexes; two of the indicators (Self-Negativity Percent and At Least One Striving) are "meta-indicators" that draw from more than one coding category and have been abandoned; and one indicator (Unusual Character Percent) is seldom used due to the rarity of the coding elements involved. For the remaining 22 HVdC indicators, the results of previous analyses were almost entirely preserved. All 12 of the statistically significant differences at the .05 level remain. Of the 11 out of 12 differences that were also significant at the .01 level, only one was "downgraded" to the p < .05 level (Domhoff & Schneider, 2015b). This change involved the rarely used Torso-Anatomy Percent, which is determined by dividing the number of torso body parts (torso, anatomy, and genitals) by the total number of body parts that are coded. (Although seldom used, this indicator can be useful in cases in which inspection of the dream reports or the situation of the dreamers suggests there may be atypical concern with body parts or body imagery; for example, it detected a concern with the body in mastectomy patients in a pre- and post- research design (Giordano, et al., 2012).) The full results of applying the Benjamini-Hochberg correction to the HVdC normative findings on men and women are displayed in Table 4.
Table 4. The Hall/Van de Castle male norms and female norms compared, with 22 p values before and after adjustment using the Benjamini-Hochberg step-up algorithm
From Domhoff & Schneider (2015b).
*p < .05 **p < .01
A second test of the strength of findings using numerous HVdC indicators was based on the results from a comparison of the women's norms with the random sample of 250 dream reports drawn from the Barb Sanders dream series, which already had been coded for characters, social interactions, misfortune/good fortune, success/failure, and emotions for substantive reasons. In all, 19 content indicators were calculated and compared with the HVdC female norms. Twelve of the 19 indicators were originally statistically significant at the .05 level; five of the 12 that were significant at the .05 level were also significant at the .01 level. After applying the Benjamini-Hochberg correction, 10 of the 12 previously significant p values remained significant at below .05, with four of five remaining significant below .01. The two measures that crossed over from significant (p < .05) to non-significant (p ≥ .05) had small effect sizes (h = .11 & h = .16) (Domhoff & Schneider, 2015b). The Necessity of Large Sample SizesSample sizes have to be large in most psychological studies to conclude anything with confidence, a point that has been demonstrated empirically as part of the concern that many results in psychology, the neurosciences, and medicine cannot be replicated (e.g., Button, et al., 2013; Nosek, 2015). According to Cohen's (1977, p. 205) detailed work on the sample sizes necessary for attaining statistical significance with varying magnitudes of differences between samples, in particular it takes a large number of observations to detect small differences with any degree of accuracy. For example, with a real difference in proportions of .20, which is roughly equivalent to an h of .40 (about as large a difference as is generally found in dream studies), 125 observations are needed to have an 80 percent chance of attaining statistical significance at the .05 level. For proportional differences of .10, it takes a sample of 502 observations to have an 80 percent chance of attaining significance at the .05 level. The empirical results presented later in this section suggest that Cohen's calculations are exactly right for dream studies with the HVdC coding system.) In the case of dream research, the need for large samples of dream reports may be even more acute for two crucial reasons. First, not all dream reports contain the elements that are the basis for HVdC content analyses. Characters, activities, objects, and settings are present in a great majority of dream reports, but friendly and aggressive social interactions appear in less than half of dream reports, which reduces the sample size in half for these HVdC content indicators (and sexual interactions, even so much as a sensual thought or kiss, appear in perhaps 10 percent of dream reports, so any individual, gender, or cross-national differences are even likely to be detected without very large samples). Second, the magnitude of the differences between the samples that are being compared is often small, as noted earlier in this document, which makes effect sizes more difficult to detect. The large size of the samples needed for statistically reliable findings in studies of dream content has been demonstrated in four separate analyses. The first study was based on numerous subsamples drawn from the 500 dream reports in the HVdC normative sample for men (Domhoff, 1996, pp. 64-67). Using three different tables of random numbers, six random samples of 250 dream reports were used to determine an "average departure" from the findings with the full sample. The results were usually within one to three percentage points of the findings for the full sample for all of the Hall and Van de Castle indicators, which suggested that 250 dream reports are adequate to replicate the norms. With 12 random samples of 125 dream reports, the average departure was within three to 10 percentage points of the findings for the full sample for frequently occurring elements, which still seems close enough to the normative findings. However, they differed by 14 to 22 percentage points with less frequent elements, which is large enough that 125 dream reports may be an absolutely minimal sample size for elements that occur relatively infrequently. At the other extreme, 60 random sets of 25 dream reports and 30 random sets of 50 dream reports had average departures from the norms that were over 10 percentage points for most indicators (Domhoff, 1996, p. 66, Table 4.7). In a second study using the same method, but based on a three-month dream series kept in the summer of 1938 by an entomologist out of his own curiosity, the overall results with the 178 dream reports with 50 or more words were compared with those from subsamples of varying sizes. (The dream series is available on DremBank.net under the name "The Natural Scientist.") This study showed that it took 100 dream reports to come within 5 percentage points of the overall findings for most indicators (Domhoff, 1996, p. 148, Table 7.9). Based on these several different results, Domhoff (1996) concluded that it takes samples of at least 100 dream reports to make comparisons using most Hall and Van de Castle indicators. Unfortunately, based on experience and analyses since that time, which are reported on below, this conclusion needs to be updated because 125 dream reports seems to be a much safer minimum sample size. These findings were replicated and refined in a third study that used the 1,000 dream reports in the men and women's normative samples to calculate the mean number of times that various elements appeared in each dream report. This calculation made it possible to estimate the approximate number of dream reports needed for statistical significance at the .05 level of confidence for effect sizes of varying magnitudes. Based on the empirical finding that the effect size h ranges from .20 to .40 for most content categories in most dream studies, it was concluded that it takes anywhere from 22 to several hundred dream reports in each sample to detect known differences at just the .05 level (Domhoff, 2003, pp. 92-94). For example, 100 dream reports are needed in each sample to detect an effect size of .20 for the male/female percent, but only 16 dream reports are needed in each sample if the effect size is .50 (Domhoff, 2003, Table 3.7). Since the magnitude of the differences between two samples on this or any other indicator usually cannot be predicted before the study is carried out, the necessity of analyzing large samples of dream reports becomes apparent. These findings are presented in detail in Table 5.
Table 5. Estimated minimum number of dream reports needed in each comparison group to find a statistically significant difference at the .05 level
The formula used to calculate these "critical n" values is as follows:
nc = 2Zc2 / h2r
Zc is the critical Z-score for significance at the desired p level (in this table, Zc=1.96), h is the hypothetical h difference (effect size) between the two groups being compared, and r is the rate at which the coding elements in question typically appear in a single dream.
(From Domhoff, 2003.)
A fourth study used approximate randomization to determine the sample sizes that are necessary to detect the six largest differences between men and women in the Hall and Van de Castle (1966) normative samples (Domhoff & Schneider, 2008a). This analysis is of special interest because the frequency of the elements that determine these various percentages and ratios, along with the magnitude of the gender differences, vary greatly from indicator to indicator. It therefore takes larger numbers of dream reports to have the necessary observations to detect differences on infrequently appearing elements that are not large in magnitude. The minimum sample size needed to replicate the original findings was defined very leniently as the point at which 50 percent of the 10 subsamples of a given size yielded a p value less than .05. This is lower than the usual standard for what is considered good statistical power, in which it is expected that there will be an 80 percent chance that the actual differences will be detected (i.e., the null hypothesis will be rejected). Based on an approximate randomization study of 10,000 pairs of resamples of the men and women's normative dream reports, with 250 dream reports in each sample, all six gender differences have a p value of .05 or lower, which is consistent with findings presented earlier in this section that 250 dream reports in each sample replicate the norms. For subsamples with 125 dream reports, five of the six differences have a p value of .05 or lower. For sample sizes below 60, four of the six indicators remain statistically significant at the .05 level or below. Gender differences for only one indicator, the M/F%, could still be detected at the .05 level or lower half the time with sample sizes as small as 30 dream reports. This was possible because the relevant elements for this indicator appear frequently and the gender difference on M/F% is very large (Domhoff & Schneider, 2008a). A fifth and final study on this issue examined the sample sizes needed to detect the five largest differences between the women's norms and the random sample of 250 dream reports from the Barb Sanders series/(Domhoff, 2003, Chapter 5; 2010). These differences concern the fact that Sanders had a very percentage of dreams with At Least One Sexuality, a high Aggressor Percent, and high rates of social interaction on both the A/C Index and the F/C Index, along with a very low Friends Percent. (The finding on her low Friends Percent is not in conflict with her high F/C Index because it is possible to have friendly interactions with family members and unknown characters while at the same time having few friendly interactions with the friends who appear in the dream reports). Based on 10,000 approximate randomization pairings created through resampling for each indicator, all five differences between the Barb Sanders sample and the normative women's sample were detected at the .05 level of significance or lower with 125 dream reports per sample. However, when only 100 reports per resample were compared, the differences on the Aggressor Percent and the A/C Index were not at or below a p value of .05 even half the time, once again suggesting 125 dream reports as a minimal sample size. The p values for the F/C Index were not at or below .05 on half of the trials when there were less than 75 dream reports in each resample. On the other hand, and confirming the larger point, it took only 25 dream reports per resample to detect the very large differences on At Least One Sexuality with a p value of .05 or lower. The even larger h difference due to her very low Friends Percent compared to the women's norms could be detected with a p value of .05 or lower with only 15 dream reports per resample. Overall, however, it would be folly to have less than 125 dream reports in a sample of a person's dreams that is going to be compared with the HVdC norms for men or women, unless the study is narrowly focused on one or two predetermined indicators that are based on elements that appear frequently and predicted to reveal very large differences. As demonstrated by these five different studies based on three different methodologies, it takes at least 125 dream reports to replicate most of the statistically significant findings that have been established using larger samples. This is 25 more dream reports than suggested in earlier work as the minimum sample size (100 dream reports), but these further analyses suggested that a new minimum needed to be established (Domhoff, 1996, 2003). It is therefore likely that the small sample sizes in numerous studies of dream content have led to many instances in which the null hypothesis has been accepted when it should have been rejected. This means that real differences that may have proven useful in theory building have been lost. Once again, both the magnitude of effect sizes and statistical power are critical (Ellis, 2010). In addition, it should be stressed that normative findings are not necessarily replicable with smaller sample sizes. Once reliable and repeated relationships are established with large sample sizes, it does not mean that they will be found with small sample sizes. The Value of ReplicationsFor all the usefulness of the various statistical tests discussed in this document, virtually all statisticians agree that there is no substitute for replication studies in psychology no matter how large the sample size or how great the sophistication of the statistical analysis. That's because no statistical test is perfect (e.g., Cohen, 1990, 1994; Cumming, 2012, 2014a, 2014b; Hunter, 1997; F. Schmidt, 1996; S. Schmidt, 2009). This admonition seems doubly important for dream research, in which contradictory results are frequent due to the many studies that have small sample sizes or employ new or untested rating scales without taking into account that many of the real differences that actually exist on several variables are small in their magnitude. It therefore makes sense to assume that any result reported in the dream literature is considered tentative until it has been replicated at least once. Moreover, once successful replications are carried out on independent samples, then in theory there is no need for a correction because multiple tests were made on the same sample. This is because replication virtually eliminates the chances that the finding involves a false rejection of the null hypothesis (a Type I error), which is what such correction formulas are designed to guard against. Bypassing the use of corrections for multiple tests, in turn, means that actual differences in future samples of adequate size are more likely to be accepted, not wrongly rejected (a Type II error), which is always a risk when using any test for multiple corrections. As already stressed in the section on multiple testing, this is due to the fact that all corrections tests have the unfortunate side effect of reducing statistical power (the ability to detect a statistically significant difference when one exists) to one degree or another. Running multiple correction tests on many small samples even could be self-defeating in that they create an unnecessary downward spiral that is a function of the tests' assumptions, not the actual findings. If there is an insistence upon repeated use of multiple corrections tests by journal editors, then researchers should use one-tailed tests because the direction of the difference can be predicted on the basis of the replicated results. The issue of validityAlong with reliability of coding, the use of appropriate statistical analyses, the use of adequate sample sizes, and replication, the key (and final) issue in terms of HVdC findings is their "validity." Do they relate to the important waking factors to which they are intended to relate? This is actually the issue of psychological meaning in a more general and abstract form. In effect, then, many of the substantive claims made about the content of dream reports based on HVdC findings are also about the validity of the HVdC coding system. Thus, the widespread evidence that findings with the HVdC coding system relate to gender, culture, age, and the differing waking personal concerns of individual dreamers, demonstrates the coding system's validity. This widespread evidence can be found in many different articles and books by dream researchers in several different countries, stretching from Canada to Iran to India and Japan,. It has led to new discoveries and its replicated findings provide a strong foundation for future theorizing about dreaming and dream content (e.g., Avila-White, et al., 1999; Crugnola, Maggiolini, Caprin, Martini, & Giudici, 2008; Domhoff, 1996, 2003; Karagianni, Papadopoulou, Kallini, Dadatsi, & Abatzoglou, 2013; McNamara, McLaren, & Durso, 2007; Strauch, 2005; Strauch & Lederbogen, 1999; Yamanaka, Morita, & Matsumoto, 1982). ReferencesAvila-White, D., Schneider, A., & Domhoff, G. W. (1999). The most recent dreams of 12-13 year-old boys and girls: A methodological contribution to the study of dream content in teenagers. Dreaming, 9, 163-171. Beck, A. T., & Hurvich, M. S. (1959). Psychological correlates of depression: I. Frequency of "masochistic" dream content in a private practice sampling. Psychosomatic Medicine, 21, 50-55. Benjamini, Y., & Hochberg, Y. (1995). Controlling the False Discovery Rate: A practical and powerful approach to multiple testing Journal of the Royal Statistical Society. Series B (Methodological), 57, 289-300. Benjamini, Y., & Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics, 29, 1165-1188. Bulkeley, K. (2012). Dreaming in adolescence: A 'blind' word search of a teenage girl's dream series. Dreaming, 22, 240-252. Bulkeley, K. (2014). Digital dream analysis: A revised method. Consciousness and Cognition, 29, 159-170. Bursik, K. (1998). Moving beyond gender differences: Gender role comparisons of manifest dream content. Sex Roles, 38, 203-214. Button, K. S., Ioannidis, J. P. A., Mokrysz, C., Nosek, B. A., Flint, J., & et, a. (2013). Power failure: Why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience, 14.5, 365-378. Cartwright, D. (1953). Analysis of qualitative material. In L. Festinger & D. Katz (Eds.), Research Methods in the Behavioral Sciences (pp. 421-470). New York: Holt, Rinehart, and Winston. Cartwright, R. (1992). Masochism in dreaming and its relation to depression. Dreaming, 2, 79-84. Clark, J., Trinder, J., Kramer, M., Roth, T., & Day, N. (1972). An approach to the content analysis of dream scales. In M. Chase, W. Stern & P. Walter (Eds.), Sleep Research (Vol. 1, pp. 118). Los Angeles: Brain Research Institute, UCLA. Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20, 37-46. Cohen, J. (1977). Statistical power analysis for the behavioral sciences. New York: Academic Press. Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Mahwah, N.J.: Erlbaum. Cohen, J. (1990). Things I have learned (so far). American Psychologist, 45, 1304-1312. Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49, 997-1003. Crugnola, C., Maggiolini, A., Caprin, C., Martini, C., & Giudici, F. (2008). Dream content of 10- to 11-year-old preadolescent boys and girls. Dreaming, 18, 201-218. Cumming, G. (2012). Understanding the new statistics: Effect sizes, confidence intervals, and meta-analysis. New York: Routlege. Cumming, G. (2014a). The new statistics: Estimation and research integrity. A six-part video lecture series with an emphasis on confidence intervals. http://www.psychologicalscience.org/index.php/members/new-statistics. Cumming, G. (2014b). The new statistics: Why and how. Psychological Science, 25, 7-29. Domhoff, G. W. (1996). Finding meaning in dreams: A quantitative approach. New York: Plenum. Domhoff, G. W. (2003). The scientific study of dreams: Neural networks, cognitive development, and content analysis. Washington, DC: American Psychological Association. Domhoff, G. W. (2010). Barb Sanders: Our best case to date. The Quantitative Study of Dreams, http://psych.ucsc.edu/dreams/Findings/barb_sanders.html(dreamresearch.net). Domhoff, G. W. (2015). Dreaming as embodied simulation: A widower dreams of his deceased wife. Dreaming, 25, 232-256. Domhoff, G. W. (2018). The Emergence of Dreaming: Mind-Wandering, Embodied Simulation, and the Default Network. New York: Oxford University Press. Domhoff, G. W., & Schneider, A. (2008a). Similarities and differences in dream content at the cross-cultural, gender, and individual levels. Consciousness and Cognition, 17, 1257-1265. Domhoff, G. W., & Schneider, A. (2008b). Studying dream content using the archive and search engine on DreamBank.net. Consciousness and Cognition, 17, 1238-1247. Domhoff, G. W., & Schneider, A. (2015a). Assessing autocorrelation in studies using the Hall and Van de Castle coding system to study individual dream series. Dreaming, 25, 70-79. Domhoff, G. W., & Schneider, A. (2015b). Correcting for multiple comparisons in studies of dream content: A statistical addition to the Hall/Van de Castle coding system. Dreaming, 25, 59-69. Dorus, E., Dorus, W., & Rechtschaffen, A. (1971). The incidence of novelty in dreams. Archives of General Psychiatry, 25, 364-368. Dudley, L., & Fungaroli, J. (1987). The dreams of students in a women's college: Are they different? ASD Newsletter, 4(6), 6-7. Dudley, L., & Swank, M. (1990). A comparison of the dreams of college women in 1950 and 1990. ASD Newsletter, 7, 3. Dunlap, W., Cortina, J., Vaslow, J., & Burke, M. (1996). Meta-analysis of experiments with matched groups or repeated measures designs. Psychological Methods, 1(2), 170-177. Ellis, P. D. (2010). The essential guide to effect sizes: Statistical power, meta-analysis, and the interpretation of research results. Cambridge, England: Cambridge University Press. Ferguson, G. A. (1981). Statistical analysis in psychology and education. New York: McGraw-Hill. Foulkes, D. (1982). Children's dreams. New York: Wiley. Foulkes, D. (1985). Dreaming: A cognitive-psychological analysis. Hillsdale, NJ: Erlbaum. Foulkes, D., Hollifield, M., Sullivan, B., Bradley, L., & Terry, R. (1990). REM dreaming and cognitive skills at ages 5-8: A cross-sectional study. International Journal of Behavioral Development, 13, 447-465. Foulkes, D., Sullivan, B., Kerr, N., & Brown, L. (1988). Appropriateness of dream feelings to dreamed situations. Cognition and Emotion, 2, 29-39. Franklin, R. D., Allison, D. B., & Gorman, B. S. (1997). Design and analysis of single-case research. Mahwah, N.J.: Erlbaum. Gaito, J. (1980). Measurement scales and statistics: Resurgence of an old misconception. Psychological Bulletin, 87, 564-567. Garcia, L. (2004). Escaping the Bonferroni iron claw in ecological studies. Oikos, 105, 657-660. Genovese, C. R. a. W., L. (2002). (2002). Operating characteristics and extensions of the FDR procedure. Journal of the Royal Statistical Society B, 64, 499-518. Giordano, A., Francese, V., Peila, E., Tribolo, A., Airoldi, M., Torta, R., et al. (2012). Dream content changes in women after mastectomy: An initial study of body imagery after body-disfiguring surgery. Dreaming, 22, 115-123. Gleason, J. H. (2013). Comparative power of the ANOVA, approximate randomization ANOVA, and Kruskal-Wallis test. Unpublished Ph.D., Wayne State University, Detroit. Hager, W. (2013). The statistical theories of Fisher and of Neyman and Pearson: A methodological perspective. Theory & Psychology, 23, 251-270. Hall, C. (1966). Studies of dreams collected in the laboratory and at home. Santa Cruz, CA: Institute of Dream Research. Hall, C. (1969a). Content analysis of dreams: Categories, units, and norms. In G. Gerbner (Ed.), The analysis of communication content (pp. 147-158). New York: Wiley. Hall, C. (1969b). Normative dream content studies. In M. Kramer (Ed.), Dream psychology and the new biology of dreaming (pp. 175-184). Springfield, IL: Charles C. Thomas. Hall, C. (1984). A ubiquitous sex difference in dreams, revisited. Journal of Personality and Social Psychology, 46, 1109-1117. Hall, C., Domhoff, G. W., Blick, K., & Weesner, K. (1982). The dreams of college men and women in 1950 and 1980: A comparison of dream contents and sex differences. Sleep, 5, 188-194. Hall, C., & Van de Castle, R. (1966). The content analysis of dreams. New York: Appleton-Century-Crofts. Hartmann, E., Rosen, R., & Rand, W. (1998). Personality and dreaming: Boundary structure and dream content. Dreaming, 8, 31-39. Hayes, J. R., & Hatch, J. A. (1999). Issues in measuring reliability: Correlation versus percentage of agreement. Written Communication, 16, 354-367. Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics, 6, 65-70. Hunt, H., Ruzycki-Hunt, K., Pariak, D., & Belicki, K. (1993). The relationship between dream bizarreness and imagination: Artifact or essence? Dreaming, 3(179-199). Hunter, J. (1997). Needed: A ban on the significance test. Psychological Science, 8(1), 3-7. Karagianni, M., Papadopoulou, A., Kallini, A., Dadatsi, A., & Abatzoglou, G. (2013). Dream content of Greek children and adolescents. Dreaming, 23, 91-96. Keller, B. (2012). Detecting treatment effects with small samples: The power of some tests under the randomization model. Psychometrika, 77, 324-338. Klingenberg, B. (2008). Regression models for binary time series with gaps. Computational Statistics and Data Analysis, 52, 4076-4090. McNamara, P., McLaren, D., & Durso, K. (2007). Representation of the self in REM and NREM dreams. Dreaming, 17 113-126. Mooney, C., & Duval, R. (1993). Bootstrapping: A nonparametric approach to statistical inference. Newbury Park, CA: Sage Publications. Moran, H. (2003). Arguments for rejecting the sequential Bonferroni in ecological studies. Oikos, 100, 403-405. Noreen, E. (1989). Computer intensive methods for testing hypotheses: An introduction. New York: Wiley & Sons. Norman, G. (2010). Likert scales, levels of measurement and the ''laws'' of statistics. Advances in Health Sciences Education: Theory and Practice, 15 625-632. Nosek, B. A. (2015). Estimating the reproducibility of psychological science. Science, aac4716. Perneger, T. (1998). What's wrong with Bonferroni adjustments. British Medical Journal, 316, 1236-1238. Reynolds, H. (1984). Analysis of nominal data. Newbury Park, CA: Sage Publications. Rosenthal, R., & Rubin, D. B. (1982). A simple general purpose display of magnitude of experimental effect. Journal of Educational Psychology, 74, 166-169. Rothman, K. J. (1990). No Adjustments Are Needed for Multiple Comparisons. Epidemiology, 1, 43-46. Schmidt, F. (1996). Statistical significance testing and cumulative knowledge in psychology: Implications for training of researchers. Psychological Methods, 1(2), 115-129. Schmidt, S. (2009). Shall we really do it again? The powerful concept of replication is neglected in the social sciences. Review of General Psychology, 13(90-110). Sherman, R., & Funder, D. (2009). Evaluating correlations in studies of personality and behavior: Beyond the number of significant findings to be expected by chance. Journal of Research in Personality, 43, 1053-1063. Smith, C. (2000). Content analysis and narrative analysis. In H. Reis & C. Judd (Eds.), Handbook Of Research Methods In Social And Personality Psychology (pp. 313-335). New York: Cambridge University Press. Snyder, F. (1970). The phenomenology of dreaming. In L. Madow & L. Snow (Eds.), The psychodynamic implications of the physiological studies on dreams (pp. 124-151). Springfield, IL: Thomas. Strauch, I. (2005). REM dreaming in the transition from late childhood to adolescence: A longitudinal study. Dreaming, 15, 155-169. Strauch, I., & Lederbogen, S. (1999). The home dreams and waking fantasies of boys and girls ages 9-15. Dreaming, 9, 153-161. Strauch, I., & Meier, B. (1996). In search of dreams: Results of experimental dream research. Albany, NY: State University of New York Press. Tonay, V. (1990/1991). California women and their dreams: A historical and sub-cultural comparison of dream content. Imagination, Cognition, and Personality, 10, 83-97. Trinder, J., Kramer, M., Riechers, M., Fishbein, H., & Roth, T. (1970). The effect of dream length on dream content. Psychophysiology, 7, 333. Uebersax, J. (1987). Diversity of decision-making models and the measurement of interrater agreement. Psychological Bulletin, 101, 140-146. Uebersax, J. (2014a). Statistical methods for diagnostic agreement: Basic Considerations. http://www.john-uebersax.com/stat/agree.htm. Uebersax, J. (2014b). Statistical Methods for Diagnostic Agreement: Kappa coefficients, A critical appraisal. http://www.john-uebersax.com/stat/kappa.htm. Van de Castle, R. (1969). Problems in applying methodology of content analysis. In M. Kramer (Ed.), Dream psychology and the new biology of dreaming (pp. 185-197). Springfield, IL: Charles C. Thomas. Wald, A., & Wolfowitz, J. (1940). On a test whether two samples are from the same population. Annals of Mathematical Statistics, 11, 147-162. Winegar, R. K., & Levin, R. (1997). Sex differences in the object representations in the dreams of adolescents. Sex Roles, 36(7-8), 503-516. Winget, C., & Kramer, M. (1979). Dimensions of dreams. Gainesville: University of Florida Press. Yamanaka, T., Morita, Y., & Matsumoto, J. (1982). Analysis of the dream contents in college students by REM-awakening technique. Folia Psychiatrica et Neurologica Japonica, 36, 33-52.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
